Anyone who has Googled “Thomas Bayes” or searched Wikipedia will have come across this picture.

Most sites helpfully note that this is not an authentic portrait. The costume is anachronistic, and the illustration first appears about two hundred years after Bayes’s death. In fact there is no known portrait of probably the greatest name in probability and statistical theory.
We know very little about Thomas Bayes.
We do know that he was the son of Joshua and Ann Bayes, and was born in London or possibly Herfordshire, most likely in 1701. In 1719, he began to study logic and theology at the University of Edinburgh. When Bayes graduated, his father was the minister of the Presbyterian meeting house in Leather Lane. By 1731, Bayes moved to Tunbridge Wells, Kent, and became the Presbyterian minister of the Mount Sion chapel.
While there, Bayes published his first known work in 1731. This is a theological rather than a mathematical text, with the rather self-explanatory title of Divine Benevolence or an Attempt to Prove That the Principal End of the Divine Providence and Government is the Happiness of His Creatures.
His second work was published anonymously in 1736. It was called An Introduction to the Doctrine of Fluxions, and a Defence of the Mathematicians Against the Objections of the Author of the Analyst.
It is an interesting work which gives a glimpse of academic debate in 18th century England. In it, Bayes contradicts the criticisms of Bishop George Berkeley (author of The Analyst), who attacked the logical foundation of Isaac Newton’s calculus (“fluxions”). It contained enough mathematics in the introduction for Bayes to be elected Fellow of the Royal Society in 1742.
In 1752, Bayes retired from his ministry, but remained in Tunbridge Wells for the rest of his life.
Now begins the most interesting chapter of Bayes’s life as a scientist. He became interested in probability. It was a race against death.
Bayes became ill and executed his will on 12th December, 1760. Most of his estate was bequeathed to his brothers, sisters, nephews, and cousins. He also divided 200 pounds between John Boyl and and a certain Reverend Richard Price.
Bayes died in Tunbridge Wells, Kent on 7th April, 1761. After his death, the Reverend Richard Price received Bayes’ manuscript on probability. Richard Price edited the manuscript and introduced Bayes’ theorem to the Royal Statistical Society.
It was called Essay Towards Solving a Problem in the Doctrine of Chances and was published in the Philosophical Transactions of the Royal Society in 1763.
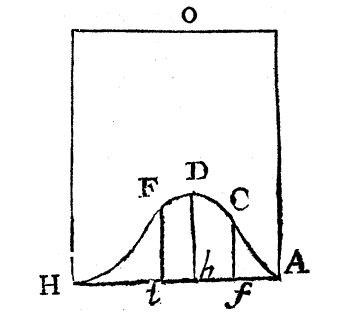
Diagram to illustrate Proposition 10 in the essay
I will leave the last word to the Revered Price himself:
Every judicious person will be sensible that the problem now mentioned is by no means merely a curious speculation in the doctrine of chances, but necessary to be solved in order to a sure foundation for all our reasonings concerning past facts, and what is likely to be hereafter. Common sense is indeed sufficient to show us that, from the observation of what has in former instances been the consequence of a certain cause or action, one may make a judgement what is likely to be the consequence of it another time and that the larger number of experiments we have to support a conclusion, so much more the reason we have to take it for granted. But it is certain that we cannot determine, at least not to any nicety, in what degree repeated experiments confirm a conclusion, without the particular discussion of the beforementioned problem; which, therefore, is necessary to be considered by any that would give a clear account of the strength of analogical or inductive reasoning; concerning, which at present, we seem to know little more than that it does sometimes in fact convince us, and at other times not; and that, as it is the means of acquainting us with many truths, of which otherwise we must have been ignorant; so it is, in all probability, the source of many errors, which perhaps might in some measure be avoided, if the force that this sort of reasoning ought to have with us were more distinctly and clearly understood.




